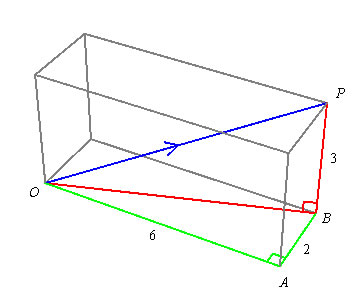
The magnitude of the vector v = 6 i + 2 j+ 3 k

Figure 1: The magnitude of the vector v = 6i + 2j + 3k
The magnitude of the vector v, written |v| or v, is the length of the arrow representing v. In Figure 1, the vector v = 6 i + 2 j+ 3 k is shown in blue. Its magnitude is the length OP. By Pythagoras in the triangle OBP, we have that OP^2=OB^2+BP^2. But by Pythagoras in the triangle OAB, we have that OB^2=OA^2+AB^2. Putting these together, we have that
and therefore that |v| = \sqrt{49} = 7.
In general, the magnitude of the vector a_1 i + a_2 j+ a_3 k is \sqrt{a_1^2+a_2^2+a_3^2}. This is sometimes called the modulus of the vector.