You're already familiar with the idea of the equation of a line in two dimensions: the line with gradient m and intercept c has equation
When we try to specify a line in three dimensions (or in n dimensions), however, things get more involved. It can be done without vectors, but vectors provide a really clear and quick way into the problem.
So, let's work in three dimensions. How much information is needed in order to specify a straight line? The answer is that we need to know two things: a point through which the line passes, and the line's direction. Both of those things can be described using vectors.

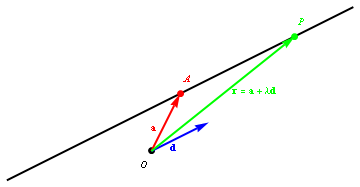
Figure 1: straight line through the point A (with position vector {\bf a}), parallel to the vector {\bf d}
Figure 1 shows the straight line through the point A (with position vector {\bf a}), parallel to the vector {\bf d}. How do we get from the origin, O, to some general point P on the line (where P has position vector {\bf r})? One answer is that we first get to the point A, by travelling along the vector {\bf a}, and then travel a certain distance in the direction of the vector {\bf d}. If the position vector of P is {\bf r}, this implies that for some value of \lambda ,
So for example, the line through the point \left(2,0,-1\right) parallel to the vector -3{\bf i}+{\bf j}-{\bf k} has equation