The scalar triple product of {\bf a}, {\bf b} and {\bf c} is defined to be $${\bf a}\cdot({\bf b}\times{\bf c}).$$ This can be shown to be equal to the determinant $$\left| \begin{array}{ccc} a_1&a_2&a_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3 \end{array} \right|.$$
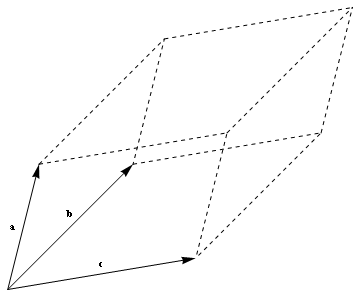
Since the volume of a parallelopiped is the area of its base multiplied by its height, the volume of the parallelopiped defined by the vectors {\bf a}, {\bf b} and {\bf c} is simply $${\bf a}\cdot({\bf b}\times{\bf c}).$$ This gives a rapid test for coplanarity: three vectors that are coplanar will have scalar triple product zero.

The parallelopiped defined by three vectors {\bf a}, {\bf b} and {\bf c}: its volume is {\bf a}\cdot({\bf b}\times{\bf c})