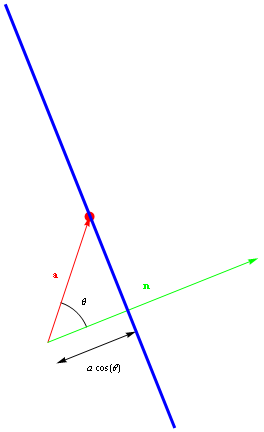
Recall that the equation of the plane through the point A with position vector {\bf a}, perpendicular to the vector {\bf n}, is $${\bf r}\cdot{\bf n}={\bf a}\cdot{\bf n}.$$ Now, $${\bf a}\cdot{\bf n}=|{\bf a}|\,|{\bf n}| \cos\theta,$$ where \theta is the angle between {\bf a} and {\bf n}. But, as the figure shows, the distance between the plane and the origin is $$|{\bf a}|\,\cos\theta.$$ It follows that given the equation of a plane, we can get the distance between it and the origin by dividing by the magnitude of the direction vector: the distance between the plane $${\bf r}\cdot{\bf n}=D$$ and the origin is $$\frac{D}{|{\bf n}|}.$$ Note that if the normal vector points away from the plane when placed at the origin, this distance will come out as negative.
Note also that if we have two parallel planes, we can calculate the distance between them by subtracting their distances from the origin.
Note finally that given a plane and a point, it's easy to calculate the distance between them, by finding the equation of the parallel plane through the point. For example, to find the distance between the plane \Pi with equation $${\bf r}\cdot(2\,{\bf i}+3\,{\bf j}-{\bf k})=5$$ and the point (-1,1,2), we first note that the plane parallel to \Pi but containing (-1,1,2) has equation $${\bf r}\cdot(2\,{\bf i}+3\,{\bf j}-{\bf k})=(-{\bf i}+{\bf j}+2\,{\bf k})\cdot(2\,{\bf i}+3\,{\bf j}-{\bf k})=-1.$$ Let's call this plane \Pi'. Now, the distance between \Pi and the origin is 5/\sqrt{4+9+1}=5/\sqrt{14}, and that between \Pi' and the origin is -1/\sqrt{14}: that is, 1/\sqrt{14} in the opposite direction. The distance between the planes is therefore 6\sqrt{14}.

Figure 1: The distance between a plane and the origin