Trigonometry: Important Angles

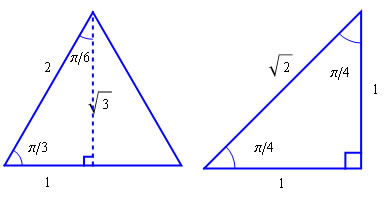
Figure 1: The 'set-square triangle'

The angles 0, \pi/6, \pi/4, \pi/3 and \pi/2 (or 0, 30, 45, 60 and 90 degrees) have sines, cosines and tangents that are worth remembering. Most of these come from the triangles shown in Figure 1. The one the left is half of an equilateral triangle of side 2. The lengths of its sides are 1, 2 and \sqrt{3} as shown, and its internal angles are \pi/6 and \pi/3 (or 30 and 60 degrees). It follows that

\begin{array}{cccccccc} \sin\pi/6&=&1/2,&\quad&\sin\pi/3&=&\sqrt{3}/2,\\ \cos\pi/6&=&\sqrt{3}/2,&\quad&\cos\pi/3&=&1/2,\\ \tan\pi/6&=&1/\sqrt{3},&\quad&\tan\pi/3&=&\sqrt{3}. \end{array}

The one on the right is an isosceles right-angled triangle whose equal sides are of length 1. The hypotenuse is therefore of length \sqrt{2} as shown, and we have that

\begin{array}{ccc} \sin\pi/4&=&1/\sqrt{2},\\ \cos\pi/4&=&1/\sqrt{2},\\ \tan\pi/4&=&1. \end{array}

The remaining "important angles" are 0 and \pi/2 (or 0 and 90 degrees). Figure 2 shows the "degenerate case": a right-angled triangle whose internal angles are close to 0 and \pi/2, and whose sides are close to 0, 1 and 1 as shown. From this degenerate triangle we get

\begin{array}{cccccccc} \sin0&=&0,&\quad&\sin\pi/2&=&1,\\ \cos0&=&1,&\quad&\cos\pi/2&=&0,\\ \tan0&=&0.&\quad&&& \end{array}

Note that \tan\pi/2 is undefined.

Figure 2: The degenerate case

The various symmetries of \sin, \cos and \tan give us a technique for handling angles greater than \pi/2. There are three principles here. One is that we measure anticlockwise from the vertical. The second is that given any acute \theta, the angles \theta, \pi-\theta, \pi+\theta and 2\pi-\theta are related: they all have the same trig ratios, differing only up to a minus sign. These related angles are shown in Figure 3. The third is this:

• In the first quadrant, between 0 and \pi/2, all the trig ratios are positive;
• In the second quadrant, between \pi/2 and \pi, only sine is positive;
• In the third quadrant, between \pi and 3\pi/2, only tangent is positive;
• In the fourth quadrant, between 3\pi/2 and 2\pi, only cosine is positive.

(The mnemonic "All Silly Tom Cats," for "All, Sine, Tangent, Cosine," may be helpful. This "positive quadrant" information is also shown in Figure 3.) So, for example, \cos 5\pi/6 must be equal either to \cos\pi/6 or to -\cos\pi/6. Because 5\pi/6 lies in the second quadrant, though, \cos5\pi/6 is negative, and

\begin{eqnarray} \cos5\pi/6&=&-\cos\pi/6\\ &=&-\sqrt{3}/2. \end{eqnarray}

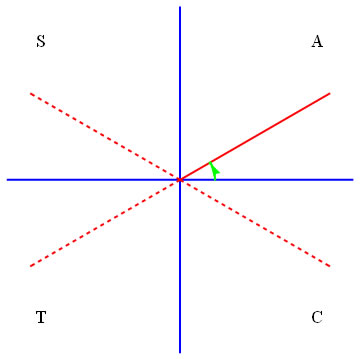
Figure 3: Angles in all quadrants