The probability of something happening can be thought of as the proportion of times it would happen if the same circumstances were rerun a large number of times.
This interpretation actually has a few problems, especially if "rerunning" isn't feasible (what do we mean by the "probability" of a one-off event?), but for many purposes it'll do.
Often, we can work out probabilities using a kind of symmetry argument. Suppose there is a set \Omega of possible outcomes, which we know (somehow) to be equally likely (we call this set the possibility space or outcome space). Suppose that we're interested in a subset A of those outcomes (we call such a subset an event). Then the probability of A occurring is the number of outcomes in A divided by the total number of outcomes in \Omega : we write
An example might be rolling a die that we know to be unbiased. In those circumstances, we can be sure that each of the outcomes 1,2,3,4,5,6 is equally likely. Let A be the event that the score is prime. Then
and
Often, though, no such "equally likely" argument is available (suppose, for example, that the die is biased). In those circumstances, we might need to estimate the probability using experiments (either with the real thing or with a good mathematical or computer model).
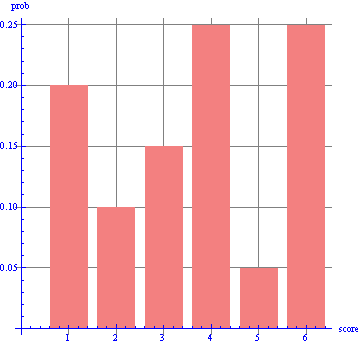
As an example, suppose we have a die that is biased so that the individual probabilities are as in the bar chart in Figure 1.

Figure 1: Probabilities of various outcomes for a biased die
Then the probability of the score being prime is simply
Notice that all the individual probabilities lie between 0 and 1, and that they add up to 1 (because one of them is bound to happen). This will always be the case.