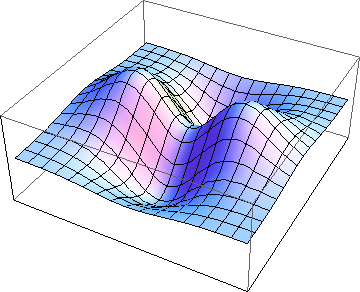
Equations of the form y = f(x) can be represented by curves in two dimensions: y, the height above the horizontal axis, varies with x, the distance along it. In equations of the form z = f(x, y), on the other hand, the height above the horizontal plane, z, varies with what you might call the "map reference'': the coordinates x and y. These equations, then, can be represented by "landscapes'' in three dimensions: what we call surfaces.

Figure 1: Surface representing a function of the form z=f(x,y)
Now, if we restrict our attention to curves, every point has a unique gradient, represented by the derivative. If you imagine yourself standing on a surface, however, the slope depends on the direction you decide to walk in. A surface that's very steep in one direction is generally much less steep in another. How can we make sense of gradient in three dimensions?
It turns out that in order to fully describe the gradient of a surface you only need two things: the gradient as you walk due East (that is, in the positive x-direction) and the gradient as you walk due North (that is, in the positive y-direction).
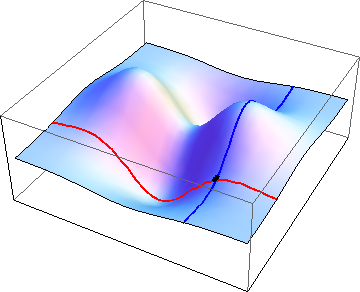
Figure 2: Surface showing "eastward'' (red) and "northward'' (blue) gradients at a point
You can get the "eastward gradient" at a point by
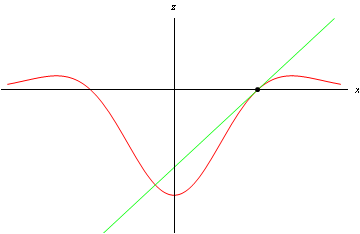
Figure 3: Curve showing "eastward'' gradient (partial derivative with respect to x)
In terms of calculation, this amounts to differentiating z with respect to x while holding the value of y constant. What you get is known as the partial derivative of z with respect to x, and is written \partial z/\partial x.
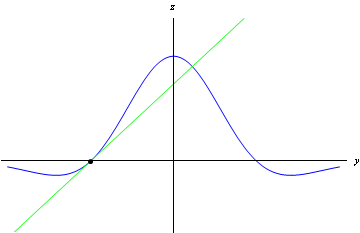
Figure 4: Curve showing "northward'' gradient (partial derivative with respect to y)
In the same way, the "northward gradient'' is obtained by differentiating z with respect to y while holding x constant. It's known as the partial derivative of z with respect to y, and is written \partial z/\partial y.
If z is represented by an explicit equation in x and y, then expressions for \partial z/\partial x and \partial z/\partial y can be calculated using the ordinary techniques of differentiation. For example: Calculate the partial derivatives of x\, y^2 + x^2 with respect to x and y, and hence find the gradient in the x-direction and the y-direction at the point (1, 2).
We start by differentiating with respect to x while treating y as a constant. The derivative of x\, y^2 with respect to x is just y^2, and the derivative of x^2 with respect to x is 2\,x. It follows that \partial z/\partial x = y^2 + 2\, x.
Similarly, the derivative of x\,y^2 with respect to y is x\times2\, y = 2\, x\, y, and the derivative of x^2 with respect to y is zero (because x, and therefore x^2, is being treated as a constant). Thus \partial z/\partial y = 2\, x\, y.
So at the point (1, 2), the gradient in the x-direction is 2^2 + 2 \times1 = 6, and the gradient in the y-direction is 2 \times1 \times2 = 4.