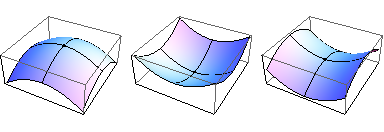
On a curve, a stationary point is a point where the gradient is zero: a maximum, a minimum or a point of horizontal inflexion. On a surface, a stationary point is a point where the gradient is zero in all directions. It turns out that this is equivalent to saying that both partial derivatives are zero

The three main types of stationary point: maximum, minimum and simple saddle
With surfaces, there are many more types-in fact, there are infinitely many types. However, all except three are very rare. A maximum is the top of a hill: the highest point in the immediate vicinity. A minimum is the bottom of a depression: the lowest point in the immediate vicinty. A simple saddle point (usually just called a saddle point) is like the pass between two mountains: it's a low point on some journeys through it, and a high point on others.
For a 3D model you can handle, and that's easy to dispose of afterwards: if you hold a Pringle crisp horizontal, there's a saddle point at the centre.
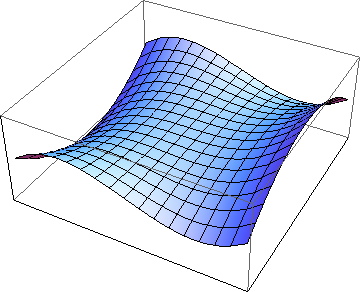
Figure 2: The monkey saddle: a non-standard type of stationary point
As we noted above, not all stationary points belong to these three categories. To be more precise about it: there are saddle points that are not simple, such the famous monkey saddle. These more complicated examples seldom crop up, however.
The techniques of partial differentiation can be used to locate stationary points. For example: Calculate the x- and y-coordinates of the stationary points on the surface given by $$z = x^3 - 8\, y^3 - 2\, x^2\, y + 4\, x\, y^2 - 4\, x + 8\, y.$$ At a stationary point, both partial derivatives are zero. That is, $$3\, x^2 - 4\, x,\ y + 4\, y^2 - 4 = 0 $$ and $$-24\, y^2 - 2\, x^2 + 8\, x\, y + 8 = 0.$$ To find the stationary points, we solve these simultaneously. This example is actually quite tricky, but we can make things a lot easier by adding two times the first to the second, giving: $$4\, x^2 - 16\, y^2 = 0. $$ From this it follows that either x = 2\, y or x = -2\, y. Substituting x = 2\, y into the first equation gives $$8\,y^2 = 4, $$ from which we deduce that y = \pm 1/ \sqrt{2}, giving the two stationary points \pm(\sqrt{2}, 1/\sqrt{2}). Substituting x = -2 y into the first equation gives $$24\,y^2 = 4, $$ which gives us y = \pm 1/\sqrt{6}, and hence the stationary points \pm (\sqrt{2/3}, - 1/\sqrt{6}). There are, therefore, four stationary points on this surface.
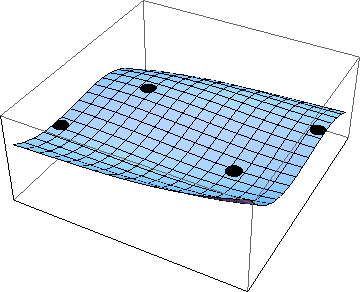
Figure 3: Stationary points on the surface z = x^3 - 8\, y^3 - 2\, x^2\, y + 4\, x\, y^2 - 4\, x + 8\, y.