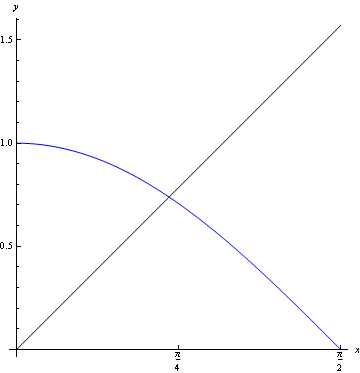

Figure 1: The graphs of y=x (black) and y=\cos x (blue) intersect
Equations don't have to become very complicated before symbolic solution methods give out. Consider for example the equation $$x=\cos x.$$ It quite clearly has at least one solution between 0 and \pi/2; the graphs of y=x and y=\cos x intersect. However, no algebraic methods exist for solving this equation.
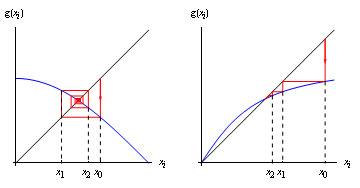
Figure: Spiral towards the root for -1< g'(\alpha)<0, and zigzag towards the root for 0< g'(\alpha<1
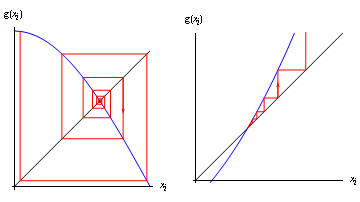
Figure 3: Spiral away from the root for g'(\alpha)<-1, and zigzag away from the root for g'(\alpha)>1
But observe the following. Let's suppose we start with an initial estimate of 0.75 as a solution of our equation. Now:
\begin{eqnarray} \cos(0.75)&=&0.731689\\ \cos(0.731689)&=&0.744047\\ \cos(0.744047)&=&0.735734\\ \cos(0.735734)&=&0.741339\\ \cos(0.741339)&=&0.737565\\ \cos(0.737565)&=&0.740108\\ \cos(0.740108)&=&0.738396\\ \cos(0.737565)&=&0.740108\\ \cos(0.740108)&=&0.738396\\ \cos(0.738396)&=&0.739549\\ \cos(0.739549)&=&0.738772\\ \cos(0.738772)&=&0.739296 \end{eqnarray}
and it's clear that our solution is approximately 0.739. However, this approach (known as fixed point iteration) doesn't always work. Consider, for example, the equation $$x=1.8\,\cos x.$$ If we start with x=1.0 as a first approximation to the solution, this is what happens:
\begin{eqnarray} 1.8\,\cos(1.0) &=& 0.972544 \\ 1.8\,\cos(0.972544) &=& 1.01376 \\ 1.8\,\cos(1.01376) &=& 0.951614 \\ 1.8\,\cos(0.951614) &=& 1.04467 \\ 1.8\,\cos(1.04467) &=& 0.903944. \end{eqnarray}
It's clear that these numbers are getting further away from any root.
So, when does fixed point iteration work and when does it fail? We can get some insight into that by looking at Taylor series.
Let \alpha be a root of the equation $$x=g(x)$$ Now, by Taylor's theorem, $$g(x)=g(\alpha)+(x-\alpha)g'(\alpha)+\dots$$ But g(\alpha)=\alpha, so we have $$g(x)-\alpha\approx g'(\alpha)\,(x-\alpha).$$ But we're iterating g: that is, evaluating it repeatedly. It follows that if our nth estimate is x_n then $$x_{n+1}=g(x_n).$$ So from the above, we have that $$(x_{n+1}-\alpha)\approx g'(\alpha)\,(x_n-\alpha).$$ In other words, the distance between our estimate and the root gets multiplied by g'(\alpha) (approximately) with each iteration. So the iteration converges if |g'(\alpha)|<1, and diverges if |g'(\alpha)|>1 (the rare case g'(\alpha)=1 can correspond either to very slow convergence or to very slow divergence). We can illustrate this diagrammatically, using the following clever idea. We plot, on the same axes, y=x and y=g(x), then do the following:
The resulting line is either a spiral (if g'(\alpha)<0) or a "staircase'' (if g'(\alpha)>0). It can easily be seen from the diagrams that the spiral is inwards provided -1< g'(\alpha)<0 and that the zigzag is towards the root if 0< g'(\alpha)<1. It can also be seen that the spiral is outwards provided g'(\alpha)<-1 and that the zigzag is away from the root if g'(\alpha)>1. Given some particular equation, there are in general several ways to set it up as a fixed point iteration. Consider, for example, the equation $$x^2=5$$ (which can of course be solved symbolically---but forget that for a moment). This can be rearranged to give $$x=\frac{x+5}{x+1},$$ suggesting the iteration $$x_{i+1}=\frac{x_i+5}{x_i+1}.$$ Alternatively, it can be rearranged to give $$x=\frac{3x^2-5}{2x},$$ suggesting the iteration $$x_{i+1}=\frac{3{x_i}^2-5}{2x_i}.$$ The first of these will work, as
\begin{eqnarray} g'(\alpha)&=&g'(\sqrt{5})\\ &=&-\frac{4}{(1+\sqrt{5})^2}\\ &=&-0.382. \end{eqnarray}
The second of these will fail, as
\begin{eqnarray} g'(\alpha)&=&g'(\sqrt{5})\\ &=&\frac{3\times(\sqrt{5})^2+5}{2\times(\sqrt{5})^2}\\ &=&2. \end{eqnarray}