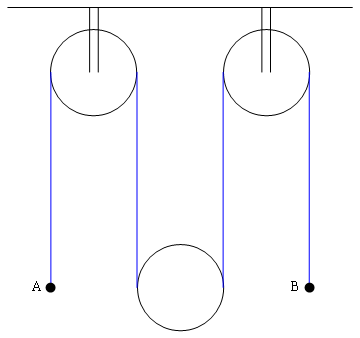
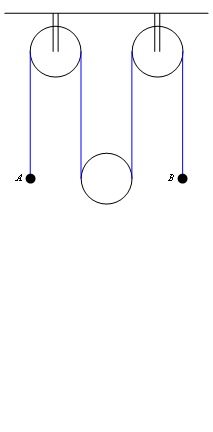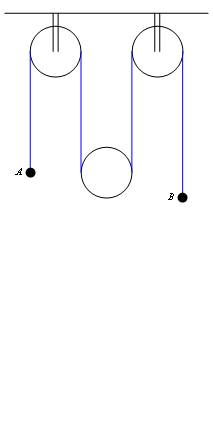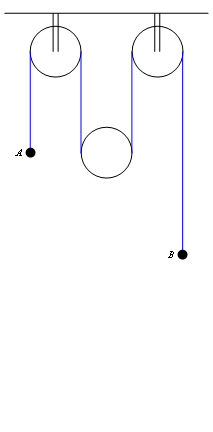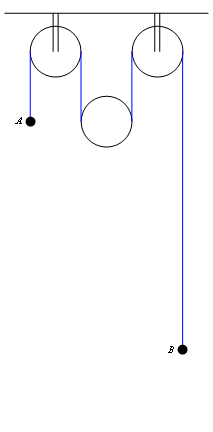
A more complicated system is shown in Figure 1. Here the free central pulley is thought of as having a mass; once again, the string is light, and all pulleys smooth.

Figure 1: system of three pulleys, two fixed and one free.
Suppose, for example, that the mass A is 1 kg, the mass B is 3 kg and the mass of the free pulley is 2 kg. Suppose that A accelerates upwards with acceleration a_{1} (if the acceleration is downwards, this will come out negative) and the B accelerates upwards with acceleration a_{2}.
Then a key observation is that the downward acceleration of the free pulley is \left(a_{1}+a_{2}\right)/2. This isn't obvious, so let's think about why it's the case.
The reason is that if the section of the string from which A is suspended shortens by x_{1} metres, and that from which B is suspended by x_{2} metres, then the central loop lengthens by \left(x_{1}+x_{2}\right) metres.
Since this loop consists of two vertical sections (and a semicircular one around the pulley whose length stays constant), this means that the pulley descends a distance of \left(x_{1}+x_{2}\right)/2 metres.
Simply differentiating twice gives us the result that the downward acceleration of the pulley is
Figure 2 shows the system with the forces and accelerations added.
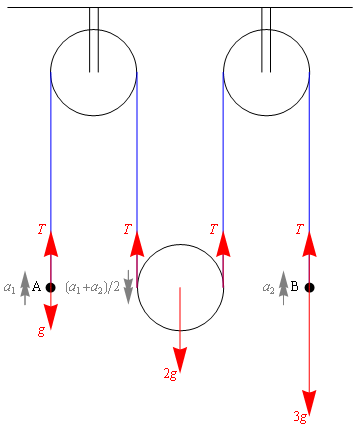
Figure 2: System of pulleys showing forces and accelerations
Balancing forces about the mass A:
Balancing forces about the mass B:
Balancing forces about the free pulley:
Subtracting the first equation from the third gives:
Adding this equation to three times the second gives
This gives us a_{2}=-3g/5. From the second equation we get that
Now, from the first equation,
Finally, the downward acceleration of the free pulley is
So all in all, the mass A accelerates upwards with acceleration g/5, the mass B accelerates downwards with acceleration 3g/5 and the free pulley accelerates upwards with acceleration g/5. This behaviour is shown in the animation.
Animation 1: Motion of a system of pulleys