The centre of mass of a shape can in general only be calculated using integration.
However, if the shape happens to be made up of rectangles and triangles, we have two facts to help us.
The first, which is kind of obvious, is that the centre of mass of a uniform rectangle is at its geometrical centre.
The second, which is less obvious, is that the centre of mass of a uniform triangle is at the point of intersection of its medians: that is, the lines joining its vertices to the midpionts of the opposite sides. Moreover, the centre of mass lies two-thirds of the way along each median.
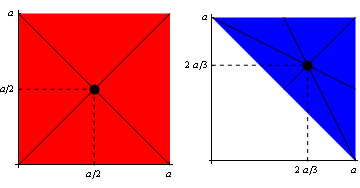
So in Figure 1, for example, the centre of mass of the red square is at the point (a/2,a/2), and that of the blue right-angled triangle is at the point (2a/3,2a/3), two-thirds of the way between, say, the vertex at (0,a) and the midpoint at (a,a/2).

Figure 1: Centre of mass of a square and a right-angled triangle.
The other fact we need is this: if a shape of mass M, whose centre of mass lies at (X,Y), is made up of smaller shapes of mass m_{1}, m_{2}, ...whose centres of mass lie at (x_{1},y_{1}), (x_{2},y_{2}), ..., then
Consider, for example, the shape in Figure 2.

Figure 2: Composite shape.
Suppose the mass per unit area of the material is \mu kilogrammes per square metre.
The rectangle from which the shape is cut has mass M=6\mu kilogrammes, and its centre of mass is at (X,Y)=(1,3/2).
The missing triangle has mass m_{1}=\frac{1}{2}\times 1\times 1\mu =\mu /2 kilogramme. The centre of mass lies two-thirds of the way between the vertex at (3/2,2) and the midpoint at (3/2,1): that is, at (3/2,4/3).
The red remnant has mass
Suppose its centre of mass is at (x_{2},y_{2}). Then
giving