Consider the matrix equation system
which can be written as the simultaneous equations
If we multiply the first of these simultaneous equations by c and the second by a, we obtain
Subtracting the first from the second gives
and hence
In a similar way, we can eliminate y; leaving out the working, what we get is
Notice that the quantity
appears in both expressions. This is a very important quantity, which is crucial to the solution process; notice, for example, that if it is zero, the elimination fails. (See the page on Gaussian elimination for a fuller discussion of what this means.)
The quantity a\,d\,-\,b\,c is known as the determinant of the matrix
written
or
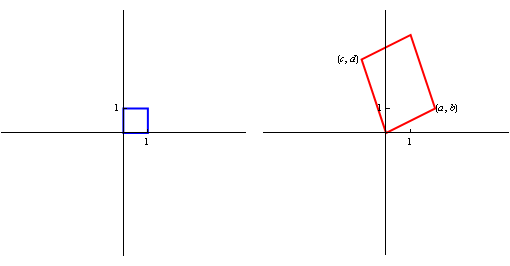
As you may know, a 2 by 2 matrix can be thought of as representing a transformation of the plane, as in Figure 1. If a shape is transformed by such a matrix, its area is always scaled up by a factor equal to the determinant. (A negative determinant implies that the transformation includes a reflection.)

Figure 1: a unit square transformed by the matrix \left(\begin{array}{cc}a&b\\c&d\end{array}\right) has its area scaled up by a\,d\,-\,b\,c.
Matrices with determinant zero, then, have the effect of flattening all shapes down on to a single line.