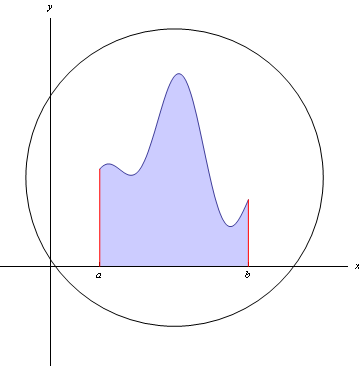
Provided f(x) is finite over the finite range a\le x \le b, the integral $$\int_a^b f(x)\,dx$$ represents an area that is what we call bounded: an area that it's possible to draw a big circle around. But there are two ways that an integral can represent an unbounded area: either the range of integration might be infinite, or the function itself might tend to infinity somewhere within, or at one edge of, the range of integration, at a point we call a singularity.
In either case we say that the integral is improper.
Now, you might think that an unbounded area is necessarily infinite, but in fact unbounded areas can be finite. Consider, for example, the improper integral $$\int_1^{\infty}\frac{1}{x^2}\,dx.$$ We define this to be the limit, as M tends to infinity, of $$\int_1^M\frac{1}{x^2}\,dx.$$ Now,
\begin{eqnarray} \int_1^M\frac{1}{x^2}\,dx&=&\left[-\frac{1}{x}\right]_0^M\\ &=&1-\frac{1}{M}, \end{eqnarray}
and of course $$\lim_{M\to\infty}\,1-\frac{1}{M}=1.$$ Another example is the integral $$\int_1^5\,\frac{1}{\sqrt{x-1}}\,dx,$$ which is improper because the integrand, 1/\sqrt{x-1}, has a singularity at x=1.
We define this to be the limit, as \epsilon tends to zero from above, of $$\int_{1+\epsilon}^5\,\frac{1}{\sqrt{x-1}}\,dx.$$ Now
\begin{eqnarray} \int_{1+\epsilon}^5\,\frac{1}{\sqrt{x-1}}\,dx&=&\left[2\sqrt{x-1} \right]_{1+\epsilon}^5\\ &=&4-2\sqrt{\epsilon}, \end{eqnarray}
and of course $$\lim_{\epsilon\to0}\,(4-2\sqrt{\epsilon})=4.$$ In general:

Figure 1: Integral of a finite function over a finite range represents a bounded
area
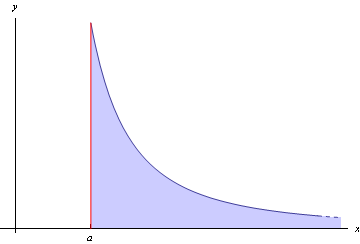
Figure 2: Integral of a finite function over an infinite range represents an unbounded
area
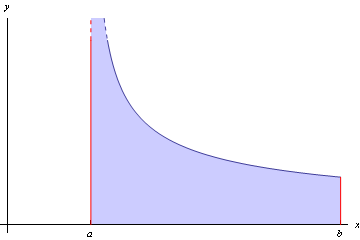
Figure 3: Integral of a function with a singularity, over a finite range, represents an unbounded
area