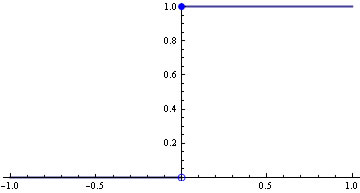
Consider the function f, where f(x)=0 if x<0 and f(x)=1 if x\geq 0. This is shown in Figure 1
. 
Figure 1: The Heaviside step function
Notice that the function jumps from 0 to 1 at x=0. It is discontinuous at x=0 and the discontinuity is 1. This is called the Heaviside function.
It's useful to know how to express other piecewise functions in terms of the Heaviside function, H(x). For example, consider the function $$f(x)=\left\{ \begin{array}{ll} 5x^2+1,&x<2,\\ 10x^2,&x\ge2, \end{array}\right.$$ shown in Figure 2
. 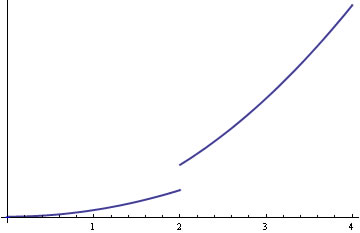
Figure 2: A piecewise function
Notice that 10x^2=(5x^2+1)+(5x^2-1), so that we can express the definition of f as follows: $$f(x)=\left\{ \begin{array}{ll} 5x^2+1,&x<2,\\ (5x^2+1)+(5x^2-1),&x\ge2. \end{array}\right.$$
Now, the function H(x-2) is equal to 0 for x<2 and 1 for x\ge 2, so the function $$(5x^2+1)+(5x^2-1)H(x)$$ is equal to 5x^2+1 for x<2 and (5x^2+1)+(5x^2-1) for x\ge 2. So f(x) can be expressed as $$f(x)=(5x^2+1)+(5x^2-1)H(x).$$