Logarithmic functions are the inverses of exponential functions. For example, note that
Another way of saying exactly the same thing is that "the logarithm to base 2 of 32 is 5"; we write:
More generally, if
then
One way of thinking of logarithms to base 2 is as answers to questions that begin "2 to the power what...?". For example, the logarithm to base 2 of 32 is the answer to the question "2 to the power what is equal to 32?" (the answer of course being 5).
More generally, the logarithm to base a of y is the answer to the question "a to the power what is equal to y"?
It's easy to show from the laws of indices that:
These are called the three laws of logarithms.
Slightly harder to prove is the change of base theorem:
(Proof: let
Then
Thus
and thus
completing the proof.)
The change of base theorem allows us to express logarithms to any base in terms of logarithms to any other base. It often makes sense, therefore, to choose a single particular base and stick to it. The one we usually choose is e=2.71828\text{...}
The logarithm to base e is called the natural logarithm, and is written \ln . The natural logarithm is the inverse of the exponential function e^{x}: if
then
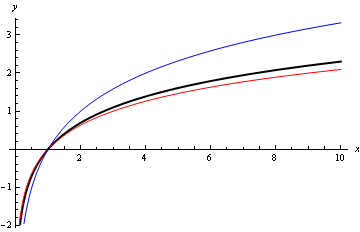
Figure 1 shows the graph of the natural logarithm, as a thick black line, together with the logarithms to base 2 and 3 (thin blue and thin red lines respectively).

Figure 1: graphs of the natural logarithm y=\,\ln \,x (thick black line), y=\text{log}_{2}x (thin blue line), y=\text{log}_{3}x (thin red line).