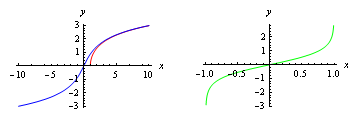
The hyperbolic sine function, \sinh x, is one-to-one, and therefore has a well-defined inverse, \sinh^{-1} x, shown in blue in the figure. In order to invert the hyperbolic cosine function, however, we need (as with square root) to restrict its domain. By convention, \cosh^{-1} x is taken to mean the positive number y such that x=\cosh y. This function is shown in red in the figure; notice that \cosh^{-1} x is defined only for x\ge 1 (at least where real numbers are concerned).

Figure 1: Plots of \cosh^{-1} x (red), \sinh^{-1} x (blue) and \tanh^{-1}
x (green)
The hyperbolic tangent function is also one-to-one and invertible; its inverse, \tanh^{-1} x, is shown in green. It is defined only for -1< x<1.
Just as the hyperbolic functions themselves may be expressed in terms of exponential functions, so their inverses may be expressed in terms of logarithms. Taking the case of \sinh first, suppose $$x=\sinh y$$. Then $$2\,x=e^y-e^{-y},$$ and hence $$e^{2y}-2\,x\,e^y-1=0.$$ Using the formula, we have $$e^y=x\pm\sqrt{x^2+1}.$$ However, since y is real, e^y must be positive, and we therefore have that $$e^y=x+\sqrt{x^2+1}.$$ Now, y=\sinh^{-1}x, and so we have $$\sinh^{-1}x = \ln(x+\sqrt{x^2+1}).$$ With \cosh, this gets a little more complicated because of the branching problem referred to above. Suppose $$x=\cosh y$$. Then $$2\,x=e^y+e^{-y},$$ and hence $$e^{2y}-2\,x\,e^y+1=0.$$ Using the formula, we have $$e^y=x\pm\sqrt{x^2-1}.$$ Now, both of these are positive, so we have $$y=\ln(x\pm\sqrt{x^2-1}).$$ However,
\begin{eqnarray} x-\sqrt{x^2-1}&=&(x-\sqrt{x^2-1})\times\frac{x+\sqrt{x^2-1}}{x+\sqrt{x^2-1}}\\ &=&\frac{x^2-(x^2-1)}{x+\sqrt{x^2-1}}\\ &=&\frac{1}{x+\sqrt{x^2-1}}, \end{eqnarray}
and therefore
\begin{eqnarray} \ln(x-\sqrt{x^2-1})&=&\ln\left(\frac{1}{x+\sqrt{x^2-1}}\right)\\ &=&-\ln(x+\sqrt{x^2-1}). \end{eqnarray}
So our solutions are $$y=\pm\ln(x+\sqrt{x^2-1}).$$ By convention we take the positive branch, and \ln(x+\sqrt{x^2-1}) is positive for x\le 1, so we have, finally, that $$\cosh^{-1}x=\ln(x+\sqrt{x^2-1}).$$ Inverting \tanh is much easier, and is left as an exercise to you: the answer is $$\tanh^{-1}x=\frac{1}{2}\,\ln\left(\frac{1+x}{1-x}\right).$$