An exponential function is a function of the form
where a is a constant.
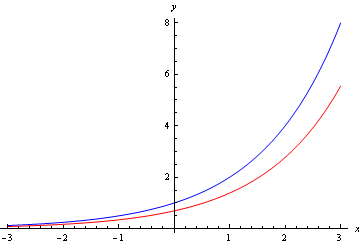
Figure 1 shows the graph of y=2^{x}, in blue, together with that of its gradient, in red. Notice that the function itself and the gradient are very similar to one another: they both rise rapidly as x gets larger.

Figure 1: graph of y=2^{x} (blue line) and its gradient (red line)
Figure 2 shows y=3^{x} together with its gradient. Again, the two curves are very similar; this time, however, the gradient curve is just slightly above that of the function itself.

Figure 2: graph of y=3^{x} (blue line) and its gradient (red line)
There is a number called e, lying between 2 and 3, such that the graph of y=e^{x} and that of its gradient are exactly the same.
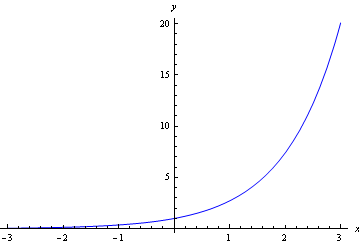
Figure 3: graph of y=e^{x}
Note that