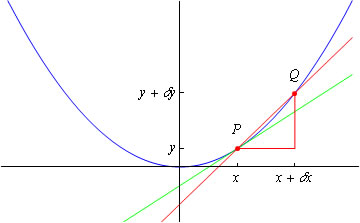
Suppose we have a smooth function f(x) which is represented graphically by a curve y=f(x) then we can draw a tangent to the curve at any point P. It is important to be able to calculate the slope of the tangent. Of course a graphical method can be used but this is rather imprecise so we use the following analytical method: We choose a second point Q on the curve which is near P and join the two points with a straight line PQ called a secant and calculate the slope of the line. Then we allow Q to approach P so that the secant swings around until it just touches the curve and becomes a tangent. The limit of the slope of the secant is the required slope of the tangent.

Figure 1. The gradient of the secant and the gradient of the tangent
We can put this more precisely and more usefully. Suppose the coordinates of P are (x,y) and the coordinates of Q are (x+\delta x,y+\delta y) so that y=f(x) and y+\delta y=f(x+\delta x). Then the slope of the secant is $$\frac{\delta y}{\delta x}=\frac{f(x+\delta x)-f(x)}{\delta x}.$$ The slope of the tangent is $$\lim_{\delta x\rightarrow 0}\frac{\delta y}{\delta x}= \lim_{\delta x\rightarrow 0}\frac{f(x+\delta x)-f(x)}{\delta x}.$$ Consider, for example, the case y=x^2. In this case, the coordinates of P and Q are (x, x^2) and (x+\delta x, [x + \delta x]^2) respectively, and the limit is
\begin{eqnarray} \lim_{\delta x\rightarrow 0}\frac{(x+\delta x)^2-x^2}{\delta x} &=&\lim_{\delta x\rightarrow 0}\frac{x^2+2x\delta x+\delta x^2-x^2}{\delta x}\\ &=&\lim_{\delta x\rightarrow 0}\frac{2x\delta x+\delta x^2}{\delta x}\\ &=&\lim_{\delta x\rightarrow 0} 2x+\delta x\\ &=&2x. \end{eqnarray}
This tells us that the gradient of the curve y=x^2 at any given point is twice that point's x-coordinate.
The limit is called the derivative of y or f(x) with respect to x and is written $$\frac{dy}{dx}$$ or $$f^\prime(x).$$ These are just different notations for the same thing.
You should be able to differentiate the following functions from the method above: