Differentiation: Stationary Points

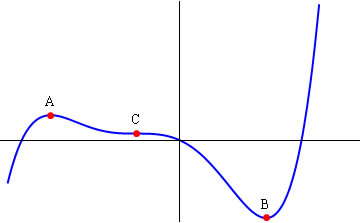
One of the points of differential calculus is to be able to tell when functions have stationary points. At these points the tangent is horizontal so the slope is zero.

Figure 1: The three types of stationary point

In order to locate such points we solve the equation $$\frac{dy}{dx}=0$$

So, for example, the stationary points on the curve $$y=2x^3-3x^2-36x+5$$ are located at the solutions of the equation $$6x^2-6x-36=0,$$ namely $x=3$ and $x=-2$.

There are several types of stationary point: several ways in which the gradient can become zero. To distinguish these types we need to know how to differentiate the function twice. If you differentiate twice you get the second derivative written in one of these ways: $$\frac{d}{dx}\left(\frac{d f}{dx}\right)=\frac{d^2 f}{dx^2}=f^{\prime\prime}(x)=f^{(2)}(x).$$ Third and higher derivatives are usually written $f^{(n)}(x)$ with $n=3$ or more to save counting dashes. You then have the following rules for a point $P$ on the curve with coordinates $(x,y)$:

1. If $f^\prime(x)=0$ and $f^{\prime\prime}(x)>0$ then there is a minimum at $P$ -- type $B$.
2. If $f^\prime(x)=0$ and $f^{\prime\prime}(x)<0$ then there is a maximum at $P$ -- type $A$.
3. If $f^\prime(x)=0$ and $f^{\prime\prime}(x)=0$ you need more information to determine the nature of $P$.
4. If $f^\prime(x)=0$ and $f^{\prime\prime}(x)=0$ but $f^{(3)}(x)\neq 0$ then there is a point of inflexion with horizontal tangent at $P$ -- type $C$.