Differential Equations: Qualitative Methods

We focus here on coupled systems: on differential equations of the form

\begin{eqnarray} \frac{dx}{dt}&=&f_1(x,y),\\ \frac{dy}{dt}&=&f_2(x,y). \end{eqnarray}

Note that neither derivative depends on the independent variable t; this class of system is called autonomous. The state of a coupled system is represented by a pair of numbers, (x,y), which in turn can be represented as a point in a 2D plane that we call phase space. Associated with each pair of numbers is a pair of time-derivatives, (\dot x, \dot y), which depend on x and y. This vector represents the velocity with which the "state point'' (x, y) moves through phase space. We can think of a coupled autonomous differential system is a flow in phase space: drop a spot of ink on to the point representing the systems initial state, and the evolution of the system through time is represented by the path that the spot traces out.

All linear systems

\begin{eqnarray} \dot x&=&a\,x+b\,y,\\ \dot y&=&c\,x+d\,y \end{eqnarray}

have a unique critical point (that is, a point where \dot x and \dot y are both zero) at the origin. To classify that critical point, first calculate the eigenvalues of the matrix $$\left( \begin{array}{cc} a&b\\c&d \end{array} \right).$$ Then:

1. If the eigenvalues are real and distinct, the critical point is either a node or a saddle.
• If both eigenvalues are positive, the critical point is an unstable node; the trajectories are tangential to the eigenvector associated with the smaller eigenvalue.
• If both eigenvalues are negative, the critical point is a stable node; the trajectories are tangential to the eigenvector associated with the numerically smaller eigenvalue.
• If the eigenvalues are of opposite sign, the critical point is a saddle; trajectories approach asymptotically the eigenvector associated with the positive eigenvalue.



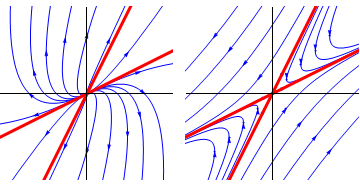
Figure 1: A node (unstable) and a saddle

2. If the eigenvalues are non-real and of the form \alpha \pm\beta\,i, the critical point is either a spiral point or a centre.
   • If \alpha>0, the critical point is an unstable spiral point.
   • If \alpha<0, the critical point is a stable spiral point.
   • If \alpha=0, the critical point is a centre.

   In all three cases, the motion is clockwise if b-c is positive and anticlockwise if it is negative.

   

   Figure 2: A centre and a spiral (unstable)

3. If the eigenvalues are real and repeated, then the critical point is either a star or an improper node. If the matrix is a multiple of the unit matrix then it is a star; if not, it is an improper node. If the eigenvalue is positive, the critical point is unstable; if negative, it is stable. In the case of improper nodes, trajectories are tangential to the sole eigenvector. If b-c is positive, then motion is clockwise; if negative, anticlockwise.

   

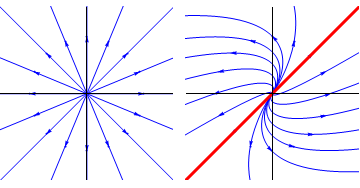
Figure 3: A star (unstable) and an improper node (unstable)