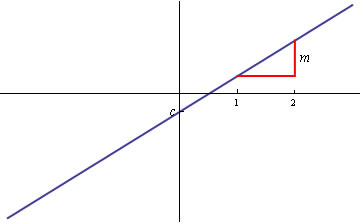
Any straight line has an equation of the form $$y = mx+c,$$ where m, the gradient, is the height through which the line rises in one unit step in the horizontal direction, and c, the intercept, is the y-coordinate of the point of intersection between the line and the y-axis. This is shown in Figure 1.

Figure 1: The straight line, y = mx + c
If we know the gradient m of a straight line with unknown intercept c, and the coordinates (x_1, y_1) of a point through which it passes, then we know that $$y_1=m x_1+c$$ and therefore $$c=y_1-m x_1.$$ If we substitute into $$y=mx+c$$ we obtain $$y=mx-mx_1+y1$$ which we can rearrange to give $$y-y_1=m(x-x_1).$$ So, for example, the straight line through the point (3,1) with gradient 2 is given by $$y-1=2(x-3),$$ which gives $$y=2x-5.$$ If we know two points (x_1, y_1) and (x_2, y_2) through which passes a line with unknown gradient m and intercept c, then
\begin{eqnarray} y_1&=&mx_1+c,\\ y_2&=&mx_2+c. \end{eqnarray}
Subtracting the first equation from the second gives $$y_2-y_1=m(x_2-x_1)$$ and therefore $$m=\frac{y_2-y_1}{x_2-x_1}.$$ The equation of the line is therefore $$y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1).$$ So, for example, the straight line through (-1,-2) and (2,7) has equation $$y+2=\frac{7+2}{2+1}(x+1),$$ which gives $$y=3x+1.$$