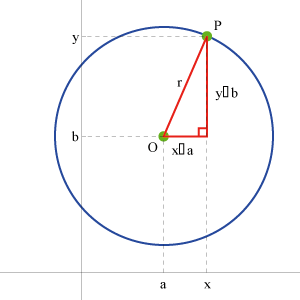
Consider a circle of radius r, centred at the point O(a,b), as in Figure 1.

Figure 1. The circle (x - a)^2 + (y - b)^2 = r^2
Consider also a point P with coordinates (x,y) on the circle. Then the distance OP is r.
By Pythagoras' Theorem, we therefore have, for all points on the circle, $$(x-a)^2+(x-b)^2=r^2.$$ This is the circle's equation.
Sometimes, we encounter the equations of circles in an expanded form. For example, consider the equation $$x^2+y^2-6x-10y+18=0.$$ Recall that $$x^2-6x=(x-3)^2-3^2$$ and $$y^2-10y=(y-5)^2-5^2,$$ and note therefore that
\begin{eqnarray} x^2+y^2-6x-10y+18=0&\Rightarrow&(x-3)^2+(y-5)^2-9-25+18=0\\ &\Rightarrow&(x-3)^2+(y-5)^2=16. \end{eqnarray}