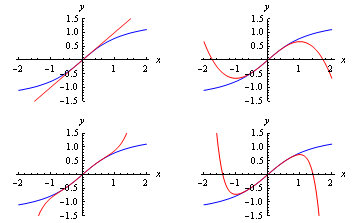
Consider a power series, $$p(x)=a_0+a_1\,x+a_2\,x^2+a_3\,x^3+\dots$$ The modulus of the ratio of successive terms is $$\left|\frac{a_{n+1}\,x^{n+1}}{a_n\,x^n}\right|=|x|\times\left|\frac{a_{n+1}}{a_n}\right|.$$ Suppose $$\left|\frac{a_{n+1}}{a_n}\right|$$ tends to some limit l. Then $$|x|\times\left|\frac{a_{n+1}}{a_n}\right|$$ tends to l\,|x|. By the Ratio Test, the power series will converge provided l\,|x|<1: that is, provided $$-\frac{1}{l}< x<\frac{1}{l}.$$ The number 1/l is known as the series' radius of convergence. If l=0 then the radius of convergence is said to be infinite. This extends in a natural way to series that do not contain all the powers of x. For example, consider the Maclaurin series for \arctan x: $$\arctan x = x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\dots+(-1)^n\frac{x^{2\,n+1}}{2\,n+1}+\dots$$ The modulus of the ratio of successive terms is $$\left|\frac{x^{2\,n+3}}{2\,n+3}\times\frac{2\,n+1}{x^{2\,n+1}}\right|,$$ which simplifies to $$x^2\,\frac{2\,n+1}{2\,n+3}.$$ The limit of this as n\to\infty is x^2, and the series therefore converges provided x^2<1: that is, provided $$-1< x<1.$$ The radius of convergence of this power series is 1. This can be clearly seen from the figure, which shows successive Maclaurin approximations to \arctan x.

Figure 1: Successive Maclaurin approximations (red) to \arctan x (blue),
showing a radius of convergence of 1