The graphs of rational functions very often have vertical asymptotes, which correspond to those points (if there are any) where the denominator becomes zero. If we want to sketch the graph of a rational function, the main things to do are
(i) to locate these vertical asymptotes by finding the values of x for which the denominator is zero;
(ii) to locate the points at which the curve crosses the x-axis, by finding the values of x for which the numerator is zero;
(iii) to find the point where the curve crosses the y-axis, by setting x=0.
(iv) to consider the sign of the function on either side of its zeros and its asymptotes
(v) to consider the behaviour of the function as x\rightarrow \pm \infty , and hence characterise any other asymptotes, horizontal or oblique, that the curve may possess.
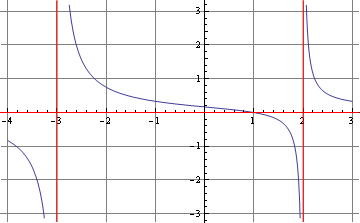
For example, consider the rational function
It has vertical asymptotes at x=2 and x=-3. It crosses the x-axis at x=1. It crosses the y-axis at
If x<-3, then \left(x-2\right), \left(x-1\right) and \left(x+3\right) are all negative, meaning that y is negative.
If -3<x<1, then \left(x+3\right) is positive, but the other two are negative, so y is positive.
If 1<x<2, only \left(x-2\right) is negative, so y is negative again.
For x>2, everything is positive, so y is positive.
Finally, the function may be rewritten as
meaning that it tends to zero as x\rightarrow \pm \infty , and therefore has a horizontal asymptote at y=0.
This is enough for us to sketch the graph of the function:

Figure 1: graph of the function y=\left(x-1\right)/[\left(x-2\right)\left(x+3\right)]
A squared factor in the numerator means that the curve just touches the x-axis. For example, consider
There are vertical asymptotes at -3and 1. The x-axis is tangent to the curve at x=-2. At x=0,
The function's values are positive for x<-3 and x>1, and negative for -3<x<1.
Finally, the function may be rewritten as
meaning that as x\rightarrow \pm \infty , y tends to 1.
This is enough for us to sketch the graph of the function:
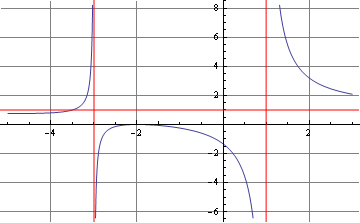
Figure 2: graph of the function y=\left(x+2\right)^{2}/[\left(x+3\right)\left(x-1\right)]
Notice that the graph has a non-zero horizontal asymptote. That's what happens when the degree of the numerator and that of the denominator are the same; when the degree of the numerator is less than that of the denominator, as in the previous example, the horizontal asymptote is always zero.
Consider the function
This is of the form "quadratic over linear". Rational functions of this type have oblique asymptotes. We can tell that by expressing them in terms of partial fractions: in the case of our example, we get
From this we can see that as x\rightarrow \pm \infty , y approaches \left(x+2\right). The graph looks like this:
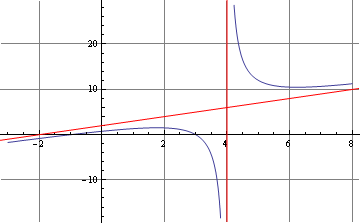
Figure 3: graph of the function y=[\left(x+1\right)\left(x-3\right)]/\left(x-4\right)