If you move the point \(P\) so that \(A\,P+B\,P\) is constant, \(P\) traces out a flattened circle shape, called an ellipse. The points \(A\) and \(B\) are the foci of the ellipse (singular focus).
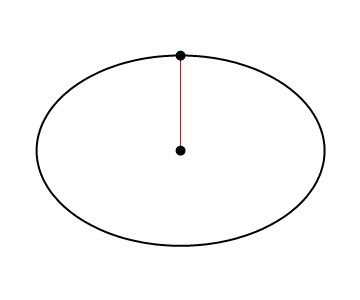
The longest distance between the centre of the ellipse and its periphery is called the semi-major axis.

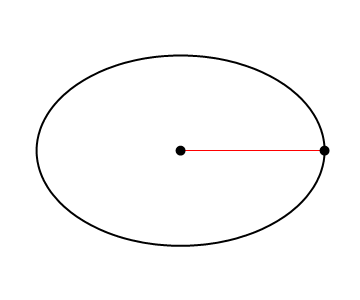
The shortest distance is called the semi-minor axis